PROBLEMA PROPUESTO, METODO HUNGARO

Solucion de costo minimo para este grafio, simple y ponderado y no dirigido.

PASO POR PASO...

Notas:

Para resolver un problema de asignacion en el cual la meta es maximizar la funcion objetivo, se debe multiplicar la matriz de ganancias por menos uno (-1) y resolver el problema como uno de minimizacion, que no es este el caso.

En un problema grande, puede resultar dificil obtener el minimo numero de filas necesarias para cubrir todos los ceros en la matriz de costos actual. Se puede demostrar que si se necesitan j lineas para cubrir todos los ceros, entonces se pueden asignar solamente j trabajos a un costo cero en la matriz actual; esto explica porque termina cuando se necesitan m lineas.

Si el numero de filas y de columnas en la matriz de costos son diferentes, el problema de asignacion esta desbalanceado. El metodo hungaro puede proporcionar una solucion incorrecta si el problema no esta balanceado; debido a lo anterior, se debe balancear primero cualquier problema de asignacion (añadiendo filas o columnas ficiticias) antes de resolverlo mediante el metodo Húngaro.
AGRÉGUE I8 E I9, para equlibrar el espacio, como se recomienda.
*I=inicio,   F= final.

PASO 1.-

Encontrar primero el elemento mas pequeño en cada fila de la matriz de costos m*m;

Se contruye una nueva matriz al restar de cada costo el costo minimo de cada fila, encontrar para esta nueva matriz, el costo minimo en cada columna.

A continuacion se debe construir una nueva matriz (denominada matriz de costos reducidos) al restar de cada costo el costo minimo de su columna.

PASO 2.-

Trazar el numero minimo de lineas (horizontales o verticales o ambas), que se requieren para cubrir todos los ceros en la matriz de costos reducidos; si se necesitan m lineas para cubrir los todos los ceros, se tiene una solucion optima entre los ceros cubiertos de la matriz. Si se requieren menos de m lineas para cubrir todos los ceros, se debe continuar con el paso 3.
Cada línea horizontal debe pasar por todo el renglón(fila) y cada línea vertical por toda la columna.

El número de lineas que se necesitaron fue 6,

como 6 es menor a m, se continua con el siguiente paso.

PASO 3.-

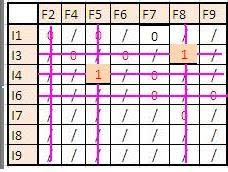Localice el número menor que no esté cubierto por una línea en la matriz de costos. Reste el valor de este número a cada elemento no cubierto por una línea y súmelo a cada elemento cubierto por dos líneas.

Por ultimo se deve regresar al paso 2.

Y NUESTRA MATRIZ DE LA SIGUIENTE MANERA:

Al cambiar de nuevo las lineas verticales y horizontales, nos damos cuenta que la cantidad es la misma que anteriormente, 6

y como 6 es menor m, continuaremos con el paso 3.

Y QUEDA ASI...

Como la cantidad de lineas aumentó al asignar los números como se indica, ahora se tiene que m es igual a 7, por lo tanto se tiene una solucion optima entre los ceros cubiertos de la matriz.

GRAFO..

Asi queda representada la matriz anterior.
Tomando en cuenta los costos que se dieron al principio del ejemplo, en la tabla de datos.